Traslazione¶

In questo capitolo si affrontano i seguenti argomenti:

Cos’è una traslazione e quali sono le sue proprietà.
Cosa sono gli elementi uniti in una traslazione.
Cosa sono le traslazioni in un poligono.
Cosa dice l’algebra sulle traslazioni.

Definizione¶

Nella geometria euclidea, una traslazione è una trasformazione che sposta tutti i punti nella stessa direzione di una distanza fissa.

In altre parole, dato un vettore, diremo che un punto P’ è il traslato del punto P se il segmento PP' ha la stessa direzione, lo stesso verso e la stessa lunghezza del vettore.

La funzione principale che realizzeremo è quella che, dato un punto e un vettore, costruisce il traslato del punto rispetto al vettore. Si dovrà poterla chiamare in questo modo:

p_1 = traslapunto(p_0, traslazione)

Ovviamente p_0 e traslazione dovranno essere rispettivamente un punto e un vettore creati precedentemente. Dopo la chiamata, p_1 conterrà il riferimento al traslato di p_0 della quantità indicata da vettore. Un frammento completo di programma potrebbe essere:

# Creo il vettore traslazione
trasl = ig.Vector(ig.Point(-13, 10, width=6),
                  ig.Point(-4, 12, width=6), name='t')

# Punto A, il suo traslato
a_0 = ig.Point(-3, 9, width=6, name="A")
a_1 = traslapunto(a_0, trasl, width=6, name="A'")

La funzione traslapunto(punto, traslazione) dovrà:

Creare una retta invisibile parallela a traslazione passante per punto.
Creare su questa retta un punto fisso nella posizione +1.
Dare come risultato questo punto.

Una possibile soluzione:

def traslapunto(punto, traslazione, **kargs):
  """Restituisce il punto traslato di traslazione."""
 parallela = ig.Parallel(traslazione, punto, False)
  return ig.PointOn(parallela, +1, **kargs)

Avviato IDLE crea una nuova finestra (menu-File-New window) e la salviamo, in una nostra cartella, con il nome trasla01_proprieta.py. Inizia questo programma con un’intestazione adeguata: alcuni commenti che contengano la data, il tuo nome e un titolo (ad esempio: Traslazioni: proprietà).

Scrivi ora un programma che disegni un vettore, un punto e il suo traslato.

Il programma potrà assomigliare a questo:

# data
# autore
# Traslazioni: proprietà

# lettura delle librerie
import pyig as ig

# funzioni
def traslapunto(punto, traslazione, **kargs):
    """Restituisce il punto traslato di traslazione."""
    parallela = ig.Parallel(traslazione, punto, False)
    return ig.PointOn(parallela, +1, **kargs)

# programma principale
ip = ig.InteractivePlane()

# Creo il vettore traslazione
trasl = ig.Vector(ig.Point(-13, 10, width=6),
                  ig.Point(-4, 12, width=6), name='t')

# Punto A e il suo punto traslato e il vettore AA'
a_0 = ig.Point(-5, 6, width=6, name="A")
a_1 = traslapunto(a_0, trasl, width=6, name="A'")
v_a = ig.Vector(a_0, a_1, width=1)

# attivazione della finestra grafica
ip.mainloop()

Esegui il programma, muovi i punti base, il punto A' deve rimanere sempre il traslato di A secondo il vettore dato. Se tutto funziona sei pronto per esplorare le caratteristiche delle simmetrie assiali.

Proprietà¶

Crea il vettore AA', con spessore 1. Esegui il programma e muovi il punto A: cosa puoi dire del segmento AA'?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci ora un nuovo punto B, il suo traslato B' e il vettore BB' (spessore 1).

Costruisci i segmenti AB e A'B' (di un colore diverso dagli altri oggetti realizzati). Visualizza le misure di AB e A'B' usando la classe VarText:

ab =ig.Segment(a_0, b_0, width=6, color='violet')
a1b1 =ig.Segment(a_1, b_1, width=6, color='violet')
ig.VarText(-7, -7, "AB = {}", ab.length())
ig.VarText(-7, -8, "A'B' = {}", ab.length())

Muovi i punti base, cosa osservi?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Puoi formulare la congettura: A'B' è congruente ad AB e prova a dimostrarla.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci un punto P vincolato al segmento AB e il suo traslato P':

p_0 = ig.ConstrainedPoint(ab, .3, width=6, color='olive drab', name="P")
p_1 = traslapunto(p_0, trasl, width=6, color='olive drab', name="P'")

Muovi il punto P, cosa osservi?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci un nuovo punto C il suo simmetrico C', costruisci il poligono ABC e il poligono A'B'C'. Cosa si può concludere circa i triangoli ABC e A'B'C'?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Cosa puoi dire sull’orientamento dei vertici del triangolo ABC e del suo trasformato A'B'C'?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Riassumendo

La traslazione è una trasformazione geometrica che trasforma segmenti in segmenti congruenti, perciò è una isometria.
La traslazione mantiene il verso dei poligoni.
Se un punto appartiene ad un segmento, il suo traslato appartiene al traslato del segmento.

Il programma completo:

# Traslazioni: proprietà

# lettura delle librerie
import pyig as ig

# funzioni
def traslapunto(punto, traslazione, **kargs):
    """Restituisce il punto traslato di traslazione."""
##    return punto + traslazione
    parallela = ig.Parallel(traslazione, punto, False)
    return ig.PointOn(parallela, +1, **kargs)

# Programma principale
ip = ig.InteractivePlane()

# Creo il vettore traslazione
trasl = ig.Vector(ig.Point(-13, 10, width=6),
                  ig.Point(-4, 12, width=6), name='t')

# Punto A e il suo punto traslato
a_0 = ig.Point(-5, 6, width=6, name="A")
a_1 = traslapunto(a_0, trasl, width=6, name="A'")
v_a = ig.Vector(a_0, a_1, width=1)

# Punto B, B', il vettore BB' e il punto medio
b_0 = ig.Point(-7, 0, width=6, name="B")
b_1 = traslapunto(b_0, trasl, width=6, name="A'")
v_b = ig.Vector(b_0, b_1, width=1)

# Segmento AB e A'B'
ab =ig.Segment(a_0, b_0, width=6, color='violet')
a1b1 =ig.Segment(a_1, b_1, width=6, color='violet')
ig.VarText(-7, -7, "AB = {}", ab.length())
ig.VarText(-7, -8, "A'B' = {}", ab.length())

# P vincolato alla retta AB
p_0 = ig.ConstrainedPoint(ab, .3, width=6, color='olive drab', name="P")
p_1 = traslapunto(p_0, trasl, width=6, color='olive drab', name="P'")

# Punto C, C' e i triangoli ABC e A'B'C'
c_0 = ig.Point(1, 5, width=6, name="B")
c_1 = traslapunto(c_0, trasl, width=6, name="A'")
ig.Polygon((a_0, b_0, c_0), width=4, color='violet', intcolor='gold')
ig.Polygon((a_1, b_1, c_1), width=4, color='violet', intcolor='gold')

# attivazione della finestra grafica
ip.mainloop()

Elementi uniti¶

Un elemento unito è un oggetto geometrico che viene trasformato in se stesso da una trasformazione.

Avvia un nuovo programma e salvarlo con il nome: trasla02_elementiuniti.py e scrivi funzione traslapunto(punto, traslazione, **kargs) che restituisce il traslato di un punto. Nel programma principale crea un punto e il suo traslato. Il programma dovrebbe assomigliare a:

# Traslazioni: elementi uniti

# lettura delle librerie
import pyig as ig

# funzioni
def traslapunto(punto, traslazione, **kargs):
    """Restituisce il punto traslato di traslazione."""
    parallela = ig.Parallel(traslazione, punto, False)
    return ig.PointOn(parallela, +1, **kargs)

# Programma principale
ip = ig.InteractivePlane()

# Creo il vettore traslazione
trasl = ig.Vector(ig.Point(-13, 10, width=6),
                  ig.Point(-4, 12, width=6), name='t')

# Punto A e il suo traslato
a_0 = ig.Point(-5, 6, width=6, name="A")
a_1 = traslapunto(a_0, trasl, width=6, name="A'")

# attivazione della finestra grafica
ip.mainloop()

Esegui il programma, muovi i punti base, se tutto funziona puoi iniziare l’esplorazione degli elementi uniti della simmetria assiale.

Sono pochi gli elementi uniti in una traslazione, solo le rette parallele al vettore traslazione. Crea:

una retta con uno spessore maggiore passante per A e parallela al vettore traslazione.
una retta con uno spessore minore e di un altro colore passante per A' e parallela al vettore traslazione.

Qualunque sia la traslazione e qualunque sia il punto A, ottieni due rette sovrapposte: cioè r' coincide con r.

Riassumendo

In una trasformazione un elemento si dice unito se viene trasformato in se stesso.
In una traslazione, sono elementi uniti solo:
- le rette . . . . . . . . . . . . . . .

Equazioni delle traslazioni¶

Un vettore è completamente determinato dalla differenza delle coordinate tra il punto iniziale e il punto finale di un segmento orientato.

Avvia una nuova finestra di editor e salvarla con il nome: trasla03_equazioni.py. In questa finestra ricopia il seguente programma:

# Traslazioni: equazioni

# lettura delle librerie
import pyig as ig

# funzioni
def traslapunto(punto, traslazione, **kargs):
    """Restituisce il punto traslato di traslazione."""
##    return punto + traslazione
    parallela = ig.Parallel(traslazione, punto, False)
    return ig.PointOn(parallela, +1, **kargs)

# Programma principale
ip = ig.InteractivePlane()

# Creo il vettore traslazione
v = ig.Vector(ig.Point(0, 0, width=6),
              ig.Point(4, 3, width=6), name='t')

# Quattro punti
a_0 = ig.Point(-5, 6, width=6, name="A")
b_0 = ig.Point(3, 6, width=6, name="B")
c_0 = ig.Point(-6, -7, width=6, name="C")
d_0 = ig.Point(7, -4, width=6, name="D")

# Lista con quattro punti
punti = [a_0, b_0, c_0, d_0]

# Vettore v applicato a tutti i punti
for punto in punti:
    v_p = ig.Vector(punto, v)

# attivazione della finestra grafica
ip.mainloop()

Esegui il programma, correggi eventuali errori. Quanti vettori vedi?

Il programma produce complessivamente cinque segmenti orientati, ma questi rappresentano un solo vettore.

È un po’ come le cinque frazioni seguenti:

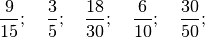
$\frac{9}{15}; \quad \frac{3}{5}; \quad\frac{18}{30}; \quad\frac{6}{10}; \quad\frac{30}{50};$

rappresentano un solo numero razionale.

Nel programma principale crea un punto P(5, 5), il suo traslato e aggiungi alcune istruzioni che visualizzino le componenti del vettore v e le coordinate del punto P e P':

# Relazione tra componenti della traslazione e
# coordinate del punto traslato
p_0 = ig.Point(5, 5, width=6, name="P")
p_1 = traslapunto(a_0, v, width=6, name="P'")

ig.VarText(-7, -10, "v = {}", v.components())
ig.VarText(-7, -11, "P = {}", p_0.coords())
ig.VarText(-7, -12, "P' = {}", p_1.coords())

Modifica il vettore v e completa la seguente tabella lasciando fisso il punto P(5, 5):

traslazione	simmetrico rispetto asse x
v (4; 3)	P’(. . . . . ; . . . . .)
v (1; -4)	P’(. . . . . ; . . . . .)
v (. . ; . . )	P’(x_p . . . ; y_p . . .)
v (a; b)	P’(. . . . . ; . . . . .)

Nella traslazione di componenti (a, b): l’ascissa del generico punto P' traslato di P è . . . . . . . . . . . . . . . ; l’ordinata del generico punto P’, è . . . . . . . . . . . . . . . .

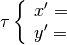
La traslazione si può tradurre nel sistema di equazioni: $\tau \left \{ \begin{array}{l} x' = \\ y' = \end{array} \right .$

Riassumendo

L’equazione della traslazione di vettore v(a; b) è: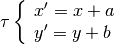

$\tau \left \{ \begin{array}{l} x' = x + a \\ y' = y + b \end{array} \right .$

Prova tu

Sul quaderno completa le seguenti frasi.

Una traslazione è
In una traslazione figure corrispondenti sono
In una traslazione sono unite
Le equazioni della traslazione di componenti (a; b) è: