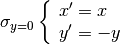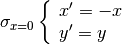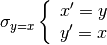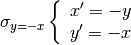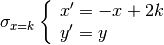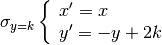Simmetria assiale¶

In questo capitolo si affrontano i seguenti argomenti:

Cos’è una simmetria assiale e quali sono le sue proprietà.
Cosa sono gli elementi uniti in una simmetria assiale.
Cosa sono gli assi di simmetria in un poligono.
Cosa dice l’algebra sulle simmetrie assiali.

Definizione¶

Una simmetria assiale di asse asse è una trasformazione che manda un punto P in un punto P' appartenente alla retta perpendicolare all'asse di simmetria in modo tale che la distanza di ``P dall’asse sia uguale alla distanza di P' dall’asse.

In altre parole, un punto P’ è simmetrico del punto P rispetto alla retta asse se il segmento PP' è perpendicolare a asse e asse taglia a metà il segmento PP'.

La funzione principale che realizzeremo è quella che, dato un punto e una retta, costruisce il simmetrico del punto rispetto alla retta. Si dovrà poterla chiamare in questo modo:

p_1 = simmpunto(p_0, asse)

Ovviamente p_0 e asse dovranno essere rispettivamente un punto e una retta creati precedentemente. Dopo la chiamata, p_1 conterrà il riferimento al simmetrico di p_0 rispetto a asse.

La funzione simmpunto(punto, asse) dovrà:

Creare una retta invisibile ortogonale a asse passante per punto.
Creare su questa retta un punto fisso nella posizione -1.
Dare come risultato questo punto.

Una possibile soluzione:

def simmpunto(punto, asse):
  """Restituisce il simmetrico di punto rispetto a asse."""
 perpendicolare = ig.Orthogonal(asse, punto, False)
  puntosimmetrico = ig.PointOn(perpendicolare, -1)
  return puntosimmetrico

La funzione proposta nel programma a fine capitolo è un po’ più concisa e, in più, usa una particolare sintassi di Python che permette di passare un numero variabile di parametri definiti per chiave.

In questo modo si possono effettuare chiamate di questo tipo:

a_1 = simmpunto(a_0, asse, name="A'")
b_1 = simmpunto(a_0, asse, name="B'", color="navy")
c_1 = simmpunto(a_0, asse, name="C'", width=7)

Avviato IDLE creiamo una nuova finestra (menu-File-New window) e la salviamo, in una nostra cartella, con il nome simass01_proprieta.py. Iniziamo questo programma con un’intestazione adeguata: alcuni commenti che contengano la data, il nostro nome e un titolo.

Il programma potrà assomigliare a questo:

# 10/9/14
# Daniele Zambelli
# Simmetrie assiali

# lettura delle librerie
import pyig as ig

# funzioni
def simmpunto(punto, asse, **kags):
    """Restituisce il simmetrico di punto rispeto a asse."""
    perpendicolare = ig.Orthogonal(asse, punto, visible=False)
    return ig.PointOn(perpendicolare, -1, **kags)

# programma principale
ip = ig.InteractivePlane()

# Creo l'asse di simmetria
asse = ig.Line(ig.Point(-3, -12, width=6),
               ig.Point(2, 10, width=6), name='asse')

# Punto A, il suo punto simmetrico
a_0 = ig.Point(-3, 9, width=6, name="A")
a_1 = simmpunto(a_0, asse, width=6, name="A'")

# attivazione della finestra grafica
ip.mainloop()

Eseguiamo il programma, muoviamo i punti base, il punto A' deve rimanere sempre simmetrico di A. Se tutto funziona siamo pronti per esplorare le caratteristiche delle simmetrie assiali.

Proprietà¶

Crea il segmento AA', con spessore 1, e costruisci il punto medio M. Esegui il programma e muovi il punto A: cosa puoi dire del segmento AA' e del suo punto medio?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci ora un nuovo punto B dalla stessa parte di A e il suo simmetrico B' rispetto alla retta asse, costruisci il segmento BB' (spessore 1) e il suo punto medio chiamandolo N. Puoi prevedere il comportamento di N?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci i segmenti AB e A'B' (di un colore diverso dagli altri oggetti realizzati). Visualizza le misure di AB e A'B' usando la classe VarText:

ab =ig.Segment(a, b, width=6, color='violet')
a1b1 =ig.Segment(a1, b1, width=6, color='violet')
ig.VarText(-7, -7, "AB = {}", ab.length())
ig.VarText(-7, -8, "A'B' = {}", ab.length())

Muovi i punti base, cosa osservi?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Puoi formulare la congettura: A'B' è congruente ad AB. Aggiungi i due segmenti: MB e MB' e prova a dimostrarla.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci un punto P vincolato al segmento AB e il suo simmetrico P':

p = ig.ConstrainedPoint(ab, .3, width=6, color='olive drab', name="P")
p1 = simmpunto(p, asse, width=6, color='olive drab', name="P'")

Muovi il punto P, cosa osservi?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci un nuovo punto C dalla stessa parte di A e B rispetto a asse e il suo simmetrico C', costruisci il poligono ABC, e il poligono A'B'C'. Cosa si può concludere circa i triangoli ABC e A'B'C'?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Cosa puoi dire sull’orientamento dei vertici del triangolo ABC e del suo trasformato A'B'C'?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Riassumendo

La simmetria assiale è una trasformazione geometrica che trasforma segmenti in segmenti congruenti, perciò è una isometria.
La simmetria assiale inverte il verso dei poligoni.
Se un punto appartiene ad un segmento, il suo simmetrico appartiene al simmetrico del segmento.

Il programma completo:

# Simmetrie assiali: proprietà

# lettura delle librerie
import pyig as ig

# funzioni
def simmpunto(punto, asse, **kags):
    """Restituisce il simmetrico di punto rispeto a asse."""
    perpendicolare = ig.Orthogonal(asse, punto, visible=False)
    return ig.PointOn(perpendicolare, -1, **kags)

# programma principale
ip = ig.InteractivePlane()

# Creo l'asse di simmetria
asse = ig.Line(ig.Point(-3, -12, width=6),
               ig.Point(2, 10, width=6), name='asse')

# Punto A, il suo simmetrico
a_0 = ig.Point(-3, 9, width=6, name="A")
a_1 = simmpunto(a_0, asse, width=6, name="A'")
# Il segmento AA' e il punto medio
sa =ig.Segment(a_0, a_1, width=1)
m = ig.MidPoint(sa, width=6, color='red', name="M")

# Punto B, il suo punto simmetrico
b_0 = ig.Point(-7, 3, width=6, name="B")
b_1 = simmpunto(b_0, asse, width=6, name="B'")
# Il segmento BB' e il punto medio
sb =ig.Segment(b_0, b_1, width=1)
n = ig.MidPoint(sb, width=6, color='red', name="N")

# Segmento AB e A'B'
ab =ig.Segment(a_0, b_0, width=6, color='violet')
a1b1 =ig.Segment(a_1, b_1, width=6, color='violet')
ig.VarText(-7, -7, "AB = {}", ab.length())
ig.VarText(-7, -8, "A'B' = {}", ab.length())
mb =ig.Segment(m, b_0, width=1)
mb1 =ig.Segment(m, b_1, width=1)

# P vincolato alla retta AB
p_0 = ig.ConstrainedPoint(ab, .3, width=6,
                          color='olive drab', name="P")
p_11 = simmpunto(p_0, asse, width=6,
                 color='olive drab', name="P'")

# Punto C, il suo punto simmetrico, i triangoli ABC e A'B'C'
c_0 = ig.Point(-10, 5, width=6, name="B")
c_1 = simmpunto(c_0, asse, width=6, name="B'")
ig.Polygon((a_0, b_0, c_0),
           width=4, color='violet', intcolor='gold')
ig.Polygon((a_1, b_1, c_1),
           width=4, color='violet', intcolor='gold')

# attivazione della finestra grafica
ip.mainloop()

Elementi uniti¶

Avvia un nuovo programma e salvarlo con il nome: simmass02_elementiuniti.py e scrivi funzione simmpunto(punto, asse, **kags) che restituisce il simmetrico di un punto rispetto a una retta. Nel programma principale crea tre punti e i loro simmetrici. Il programma dovrebbe assomigliare a:

# Simmetrie assiali: elementi uniti

# lettura delle librerie
import pyig as ig

# funzioni
def simmpunto(punto, asse, **kags):
    """Restituisce il simmetrico di punto rispeto a asse."""
    perpendicolare = ig.Orthogonal(asse, punto, visible=False)
    return ig.PointOn(perpendicolare, -1, **kags)

# programma principale
ip = ig.InteractivePlane()

# Creo l'asse di simmetria
asse = ig.Line(ig.Point(-3, -12, width=6),
               ig.Point(2, 10, width=6), name='asse')

# Punto A, B, C e i loro simmetrici A', B', C'
a_0 = ig.Point(-3, 9, width=6, name="A")
b_0 = ig.Point(-7, 3, width=6, name="B")
c_0 = ig.Point(-9, 6, width=6, name="C")
a_1 = simmpunto(a_0, asse, width=6, name="A'")
b_1 = simmpunto(b_0, asse, width=6, name="B'")
c_1 = simmpunto(c_0, asse, width=6, name="B'")

# attivazione della finestra grafica
ip.mainloop()

Esegui il programma, muovi i punti base, se tutto funziona puoi iniziare l’esplorazione degli elementi uniti della simmetria assiale.

Sposta uno dei punti sulla retta asse. Cosa osservi?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

In una trasformazione geometrica un punto viene detto unito se, trasformato, corrisponde a se stesso. Puoi concludere che:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

In generale, in una trasformazione geometrica, una figura viene detta unita quando è trasformata in se stessa (anche se non ogni suo punto è unito).

Un segmento che ha gli estremi su asse è . . . . . . . . . . . . . . . . . rispetto alla simmetria e è costituito da . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci un triangolo ABC e il suo simmetrico A'B'C'. Muovi i punti ABC in modo che il triangolo simmetrico si sovrapponga al triangolo A'B'C'. Come deve essere il triangolo ABC per essere unito rispetto alla simmetria?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Costruisci e descrivi altri elementi uniti rispetto alla simmetria.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Riassumendo

In una trasformazione un elemento si dice unito se viene trasformato in se stesso.
In una simmetria assiale sono elementi uniti:
- i punti . . . . . . . . . . . . . . .
- i segmenti . . . . . . . . . . . . . . .
- le rette . . . . . . . . . . . . . . .
- le circonferenze . . . . . . . . . . . . . . .
- i triangoli . . . . . . . . . . . . . . .
- i poligoni . . . . . . . . . . . . . . .

Poligoni simmetrici¶

Avvia un nuovo programma e salvarlo con il nome: simass03_poligoni.py. Scrivi la solita funzione simmpunto.

Scrivi una funzione che, dati centro, vertice e numlati, costruisca il poligono regolare. Lo schema potrebbe essere:

def polreg(centro, vertice, numlati, **kargs):
    """Restituisce un poligono regolare
       dati il centro un vertice e il numero di lati."""
    # crea la circonferenza su cui sono disposti i vertici non visibile
    # calcola la lunghezza dell'arco tra due vertici consecutivi
    # crea la lista dei vertici che contiene quello dato come argomento
    # aggiungi alla lista dei vertici tutti gli altri
    # restituisci il poligono costruito con questi vertici

Scrivi la funzione che, dati poligono e asse, costruisca il poligono simmetrico. Lo schema potrebbe essere:

def simmpoli(poligono, asse, **params):
    """Restituisce il simmetrico di un poligono rispetto a asse."""
    # crea una lista vuota che conterrà i vertici del poligono simmetrico
    # per ogni vertice del poligono originale, calcola il simmetrico e
    # aggiungilo alla lista dei vertici simmetrici
    # restituisci il poligono costruito con questi vertici

Nel programma principale crea:

un piano interattivo;
crea il punto O di coordinate (6, 3);
l’asse passante per quel punto e il punto (6, 7);
il triangolo equilatero di centro O e passante per (4, 3), usa la funzione polreg;
il simmetrico del triangolo (usa la funzione simmpoli).

Una figura è simmetrica rispetto ad un asse se resta unita nella simmetria.

Agendo con il mouse, muovi la retta asse facendo in modo che il triangolo trasformato si sovrapponga al triangolo originale.

Sono tre e sono quelle in cui l’asse passa per . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Ripeti le operazioni precedenti disegnando un quadrato nel secondo quadrante, un pentagono regolare nel terzo e un esagono regolare nel quarto, sempre con un asse di simmetria passante per il centro. Cosa puoi osservare?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Riassumendo

Una figura si dice simmetriche se esiste una simmetria che la trasforma in se stessa.
Una figura può avere più assi di simmetria.
I poligoni regolari hanno tanti assi di simmetria quante sono i lati del poligono.

La funzione polreg(centro, vertice, numlati, **kargs) può essere realizzata in questo modo:

def polreg(centro, vertice, numlati, **kargs):
    """Restituisce un poligono regolare
       dati il centro un vertice e il numero di lati."""
    # crea la circ. su cui sono disposti i vertici non visibile
    circ = ig.Circle(centro, vertice, visible=False)
    # calcola la lunghezza dell'arco tra due vertici consecutivi
    arco=2./numlati
    # crea la lista dei vertici che contiene l'argomento vertice
    vertici=[vertice]
    # aggiungi alla lista dei vertici tutti gli altri
    for cont in range(1, numlati):
        vertici.append(ig.PointOn(circ, cont*arco))
    # restituisci il poligono costruito con questi vertici
    return ig.Polygon(vertici, **kargs)

La funzione simmpoli(poligono, asse, **kargs) può essere realizzata in questo modo:

def simmpoli(poligono, asse, **kargs):
    """Restituisce il simm. di un poligono rispetto a asse."""
    # crea una lista vuota che conterrà i vertici
    # del poligono simmetrico
    vertici_simm=[]
    # per ogni vertice del poligono originale, calcola il
    # simmetrico e aggiungilo alla lista dei vertici simmetrici
    for vertice in poligono.vertices:
        vertici_simm.append(simmpunto(vertice, asse))
    # restituisci il poligono costruito con questi vertici
    return ig.Polygon(vertici_simm, **kargs)

Equazioni di alcune simmetrie assiali¶

Avvia un nuovo programma e salvarlo con il nome: simmas04_equazioni.py. Scrivi la solita funzione simmpunto.

Nel programma principale crea:

un piano interattivo;
una retta x sovrapposta all’asse x;
una retta y sovrapposta all’asse y;
un punto P e visualizza le sue coordinate;
il punto P' simmetrico di P rispetto all’asse x e visualizza le sue coordinate;
il punto P'' simmetrico di P rispetto all’asse y e visualizza le sue coordinate;
muovi il punto P in varie posizioni e completa la seguente tabella:

punto	simmetrico rispetto asse x	simmetrico rispetto asse y
A (-4; 3)	A’(. . . . . ; . . . . .)	A’‘(. . . . . ; . . . . .)
B (1; -4)	B’(. . . . . ; . . . . .)	B’‘(. . . . . ; . . . . .)
C (. . ; . . )	C’(. . . . . ; . . . . .)	C’‘(. . . . . ; . . . . .)
P (x; y)	P’(. . . . . ; . . . . .)	P’‘(. . . . . ; . . . . .)

Nella simmetria rispetto all’asse delle x: l’ascissa del generico punto P’ simmetrico di P è . . . . . . . . . . . . . . . all’ascissa di P; l’ordinata del generico punto P’, è . . . . . . . . . . . . . all’ordinata di P.

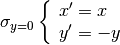
La simmetria rispetto all’asse x si può tradurre nel sistema di equazioni: $\sigma_{y = 0} \left \{ \begin{array}{l} x' = x \\ y' = -y \end{array} \right .$

Nella simmetria rispetto all’asse delle y:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

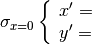
La simmetria rispetto all’asse y si può tradurre nel sistema di equazioni: $\sigma_{x = 0} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

Modifica il programma in modo che gli assi di simmetria coincidano con le bisettrici dei quadranti, muovi il punto P e completa la seguente tabella:

punto	simm. bis. I quadrante	simm. bis. II quadrante
A (-7; 3)	A’(. . . . . ; . . . . .)	A’‘(. . . . . ; . . . . .)
B (5; -2)	B’(. . . . . ; . . . . .)	B’‘(. . . . . ; . . . . .)
C (. . ; . . )	C’(. . . . . ; . . . . .)	C’‘(. . . . . ; . . . . .)
P (x; y)	P’(. . . . . ; . . . . .)	P’‘(. . . . . ; . . . . .)

Nella simmetria rispetto alla bisettrice del 1° e 3° quadrante: l’ascissa del generico punto P’, simmetrico di P è . . . . . . . . . . . . . . . . . . . . . . . . . . P; l’ordinata del generico punto P’, è . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

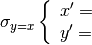
La simmetria rispetto alla bisettrice del 1° e 3° quadrante si può tradurre nel sistema di equazioni: $\sigma_{y = x} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

Nella simmetria rispetto alla bisettrice del 2° e 4° quadrante:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

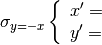
La simmetria rispetto alla bisettrice del 2° e 4° quadrante si può tradurre nel sistema di equazioni: $\sigma_{y = -x} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

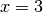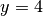Modifica la funzione test in modo che gli assi di simmetria siano le rette di equazioni: $x=3$ e $y=4$ . Muovi il punto P e completa la seguente tabella:

punto	simm. x = 3	simm. bis. y = 4
A (-6; 3)	A’(. . . . . ; . . . . .)	A’‘(. . . . . ; . . . . .)
B (4; -2)	B’(. . . . . ; . . . . .)	B’‘(. . . . . ; . . . . .)
C (. . ; . . )	C’(. . . . . ; . . . . .)	C’‘(. . . . . ; . . . . .)
P (x; y)	P’(. . . . . ; . . . . .)	P’‘(. . . . . ; . . . . .)

Nella simmetria rispetto alla retta x=3: l’ascissa del generico punto P’, simmetrico di P è . . . . . . . . . . . . . . . . . . . . . . . . . . P; l’ordinata del generico punto P’, è . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

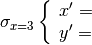
La simmetria rispetto alla retta x=3 si può tradurre nel sistema di equazioni: $\sigma_{x = 3} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

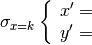
In generale la simmetria rispetto alla retta x=k si può tradurre nel sistema di equazioni: $\sigma_{x = k} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

L’equazione di questa simmetria funziona anche se k=0? Cosa puoi osservare?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Nella simmetria rispetto alla retta y=4

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

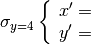
La simmetria rispetto alla retta y=4 si può tradurre nel sistema di equazioni: $\sigma_{y = 4} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

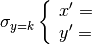
In generale la simmetria rispetto alla retta y=k si può tradurre nel sistema di equazioni: $\sigma_{y = k} \left \{ \begin{array}{l} x' = {} \\ y' = {} \end{array} \right .$

L’equazione di questa simmetria funziona anche se k=0? Cosa puoi osservare?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Riassumendo

Certe simmetrie assiali possono essere tradotte con un sistema di equazioni abbastanza semplice.
$\sigma_{y = 0} \left \{ \begin{array}{l} x' = x \\ y' = -y \end{array} \right .$

$\sigma_{x = 0} \left \{ \begin{array}{l} x' = -x \\ y' = y \end{array} \right .$
$\sigma_{y = x} \left \{ \begin{array}{l} x' = y \\ y' = x \end{array} \right .$

$\sigma_{y = -x} \left \{ \begin{array}{l} x' = -y \\ y' = -x \end{array} \right .$
$\sigma_{x = k} \left \{ \begin{array}{l} x' = -x + 2k \\ y' = y \end{array} \right .$

$\sigma_{y = k} \left \{ \begin{array}{l} x' = x \\ y' = -y + 2k \end{array} \right .$

Prova tu

Sul quaderno completa le seguenti frasi.

Una simmetria assiale (s.a.) è
In una s.a. figure corrispondenti sono
In una s.a.:
1. sono punti uniti
2. sono rette unite
3. sono segmenti uniti
4. esiste una retta formata da tutti punti uniti, è:
I poligoni regolari hanno tanti assi di simmetria ...
Assi di simmetria...
1. il cerchio ha
2. il rettangolo ha
3. il rombo ha
4. il triangolo isoscele ha
5. il trapezio isoscele ha
6. Un parallelogramma che non sia rombo o rettangolo
Le equazioni della s.a.
1. rispetto all’asse x
2. rispetto all’asse y
3. rispetto alla bisettrice del 1° e 3° quadrante
4. rispetto alla bisettrice del 2° e 4° quadrante